2024.10.25
皆さんはトポロジー最適化という言葉を聞いたことはありますか?3DプリンタやCAD、CAEを使っていると、耳にする機会も多いかと思います。なんとなく聞いたことはあるけど、詳しくは分からないという方に向けて、本記事ではトポロジー最適化について解説します。
トポロジー最適化と似た言葉で構造最適化というものがありますが、トポロジー最適化は構造最適化のうちの1つです。構造最適化は他にも複数の手法があるので、まずはどのような種類があるのかということについて説明したいと思います。
構造最適化は主に下記の寸法最適化、形状最適化、トポロジー最適化の3種類に分類されることが多いです。次にそれぞれの手法の特徴を見ていきましょう。
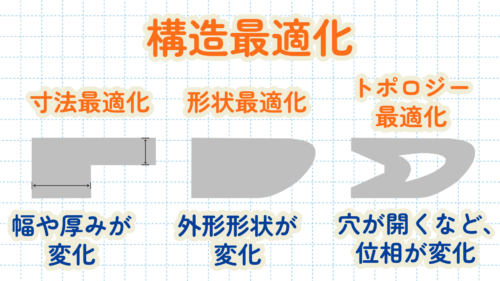
寸法最適化はその名前の通り、与えられた形状の中で部品の幅や高さなどの寸法を最適化する手法です。
例えば作成している部品が指定した荷重に耐えられるように、板厚や梁の幅を調整することがあげられます。
定義したパラメータを調整する手法のために、定義していない場所は変更されず、他の構造最適化手法と比べると設計上の自由度は低くなっています。
形状最適化は部品の外形形状を変形させて、最適化を行う手法です。
部品の境界部分を動かして調整するため、もともとモデルに穴が開いる場合はその形が大きくなったり、四角だった形状が丸になったりといった変化もあります。
ですが、次に説明するトポロジー最適化のように、穴がない形状に穴が開くということはありません。
皆さんはドーナッツとコーヒーカップが位相幾何学(トポロジー)的には同じという話を聞いたことはありますでしょうか。
ドーナッツには中心に1つの穴が開いており、マグカップには持ち手の部分に同様に1つの貫通した穴が開いて、そのほかの部分はつながっているという点で同じであると考えられます。
今回扱っているトポロジー最適化もこのような位相を最適化する方法になります。そのため、これまで紹介した寸法最適化や形状最適化と比べ設計上の自由度が高く、塊だったモデルに穴が開くなどの位相の変化が生じます。これによって、従来では考えられなかった新しい形状のデザインが可能になります。
なお、日本語では同じ”位相”ですが「位相がπ/2ずれる」などといったPhaseの和訳の位相とは違います。
トポロジー最適化が構造最適化の1種であると説明しましたが、そのトポロジー最適化の方法も1つではなく、様々なアプローチが提案されています。ここではその中でもよく使われる均質化法、密度法、レベルセット法の3種類について説明します。
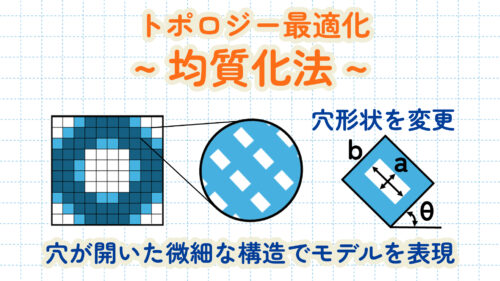
均質化法は下図のように、穴が開いた微細な構造でモデルを表現し、その穴の大きさによって各要素の密度を表します。
例えば、ある荷重に耐えられるようにトポロジー最適化を行う場合は、必要な領域はこの穴の大きさは0に近くなり、必要ない領域はこの穴が最大の大きさになります。
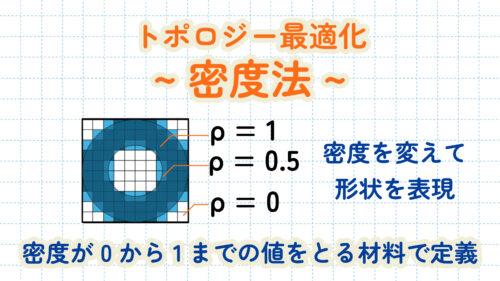
密度法では密度が0から1までの値をとる仮想的な材料で満たされていると定義し、同様に計算を行います。
その結果、密度0の領域は空洞の状態、密度1は完全に中が詰まった状態、密度0.5など間の値はその中間の状態というように定義します。この中間的な材料は現実には表現ができないので、閾値を任意に決めるなど中間領域の扱いに気を付ける必要があります。
プログラムの実装も容易な方式で、現在様々な市販ソフトウエアでこの方法が使われています。
これまで紹介した均質化法や密度法ではグレースケールと呼ばれる中間的な密度の領域ができてしまいます。
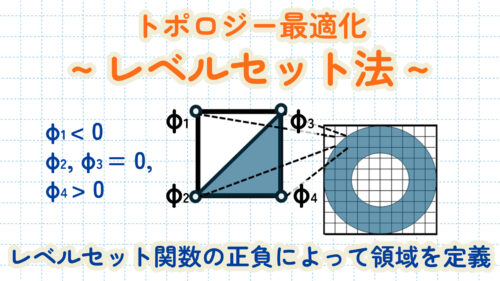
それを解決する方法としてレベルセット法が提案されています。この方法ではレベルセット関数と呼ばれる関数を定義し、この関数の正負によって領域を定義します。
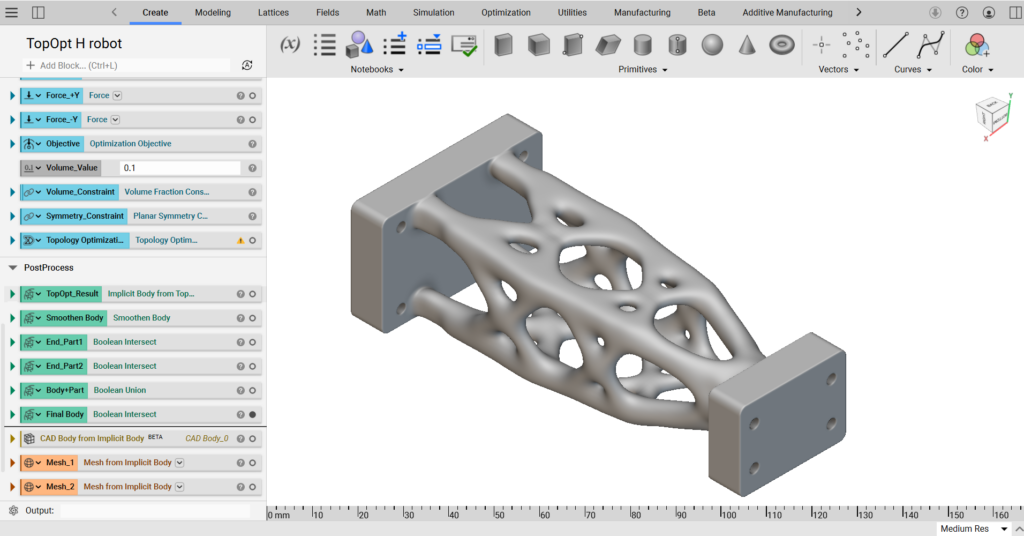
次に弊社で実施した事例をもとにトポロジー最適化の流れをご紹介します。
こちらは弊社取り扱いのモデリングソフトウエア「nTop」を使って小型ロボットのアーム部分をトポロジー最適化した事例になり、25%の軽量化に成功しました。
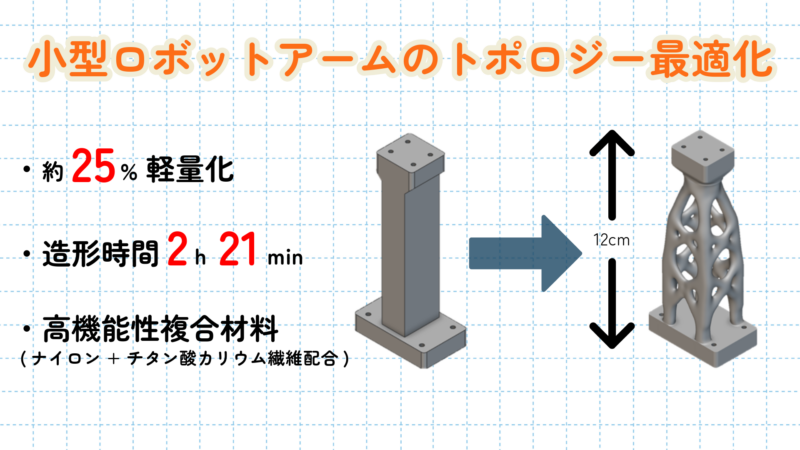
もしnTopに興味を持たれた方はこちらの製品ページもご参考ください。
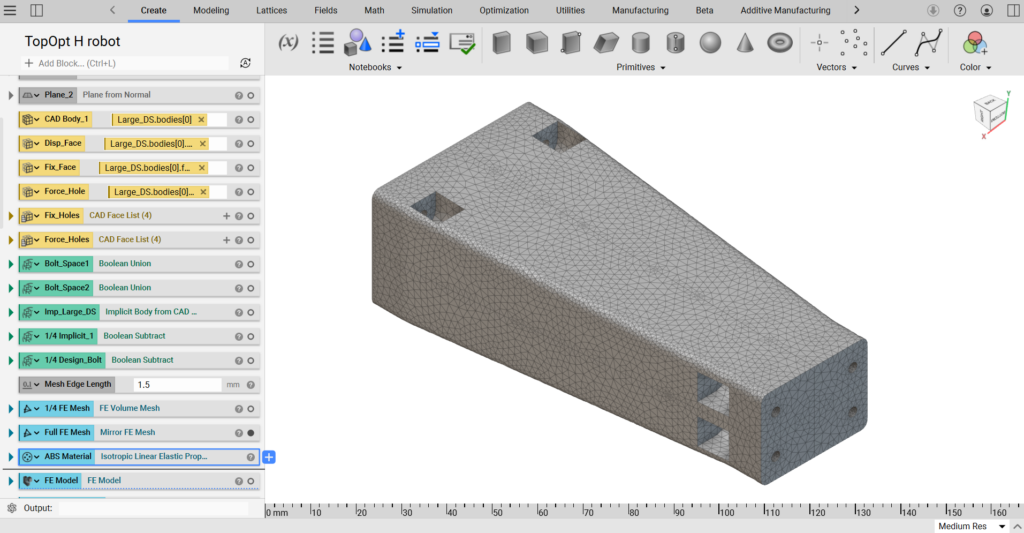
まずはデザインスペースを設計します。このデザインスペースが十分な大きさがないとトポロジー最適化後の形状も大きく制約を受けてしまうため、今回は元のモデルよりも大きなエリアを作成しました。
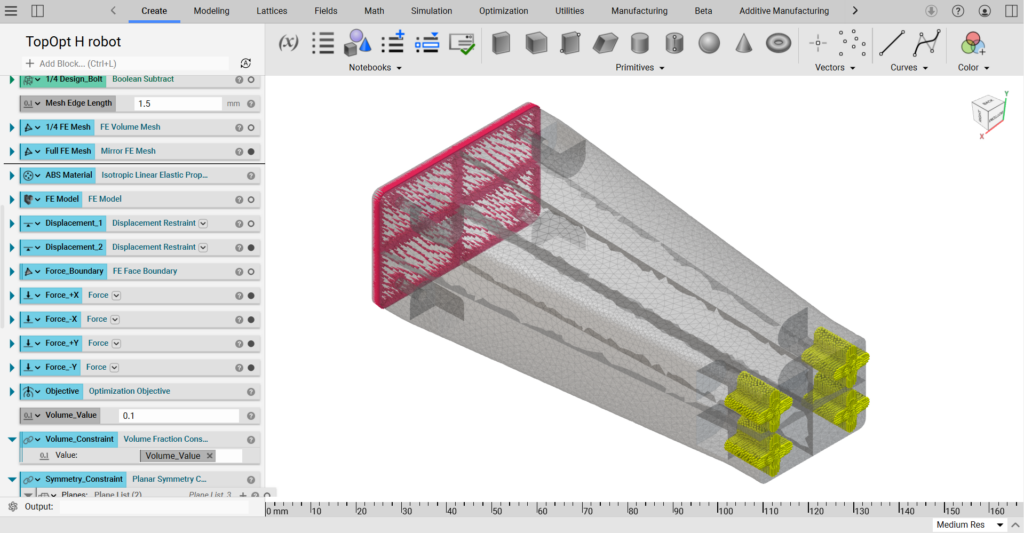
この例では線形解析の範囲でのトポロジー最適化を行うために、通常の解析の時と同様に拘束条件と荷重条件を設定します。下の図の赤色で示した一方の面に拘束の設定をして、反対の面に+X/-X, +Y/-Yのいずれか一方向から500Nの荷重がかかると設定しました。
今回は線形静解析をベースに最適化を行いましたが、近年では流体解析をベースにトポロジー最適化をおこなえるなど様々なソフトウエアが販売されています。
目的は「剛性を最大にする」というものを用いることが多く、それ以外にも「応力を最小にする」や「変位を最小にする」などの設定をします。今回は剛性の最大化を目的に設定しました。
続いて制約の設定です。何も制約がないと、元の形状が一番剛性が高いので、何かしらの制約を定義する必要があります。よく用いられる条件としては体積制約で、上記の目的関数と組み合わせると、 ”体積30%以下という条件のもと、剛性が最大になるように計算してください” ということになります。今回は体積制約に加えて、左右上下が対称になるように対称制約を設定しました。
これで設定ができましたので、あとはトポロジー最適化を実行すると、計算をもとに形状が作られていきます。
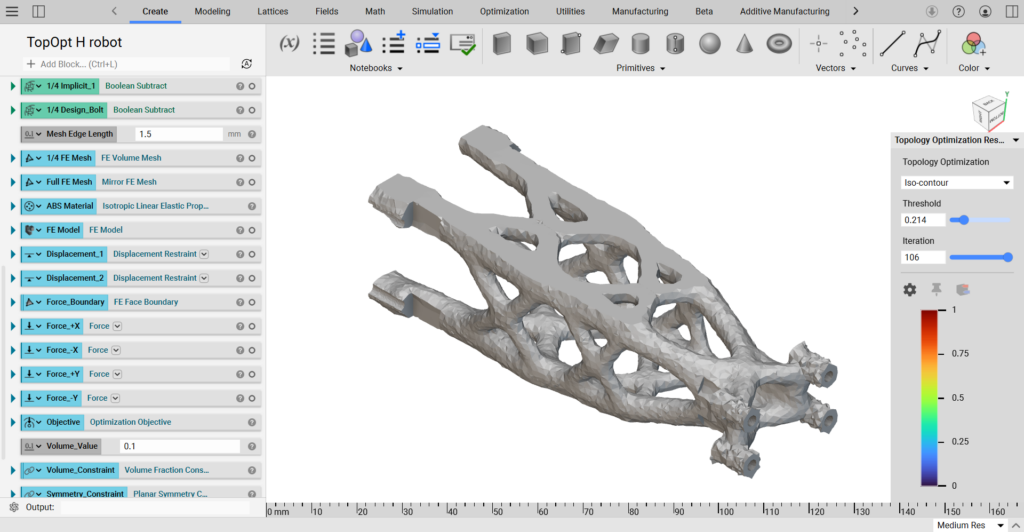
上記まででトポロジー最適化としては完成しましたが、この後3Dプリンタで出力する場合などはメッシュのざらつきがあったり、部品の取り付け部が無くなっていますので、後処理としてスムージング処理や取付面を付けたりします。
場合によっては後処理をしたモデルに対してCAEなどで強度解析を行うことも多いです。
トポロジー最適化は制約などの条件にもよりますが、有機的で複雑な形状が出来上がるため、従来の加工方法で作ろうとすると難しいことが多く、3Dプリンタで作成するケースが多いです。今回は弊社取り扱い国産3DプリンタG-ZEROにて造形を行いました。こちらはスーパーエンプラも出力可能なFFF方式の3Dプリンタです。詳しい製品情報は下記URLをご参考ください。

では実際にトポロジー最適化を使うにあたり注意しなくてはいけない点などを見ていきたいと思います。
トポロジー最適化のメリットとしては、以下の3つが挙げられます。
特に軽量化は、輸送費の削減や、自動車・航空宇宙の分野であれば燃費向上にも繋がるため、重要視されています。
一方、デメリットもあるので注意が必要です。
まだ新しい技術ですので、実際に新製品などに適用する場合は、信頼性試験の確立や実施にコストがかかることもあるかもしれません。
今回トポロジー最適化に使用したソフトウエアは、弊社で取り扱っているnTopです。nTopは3Dプリンタ向けのデザインソフトウエアで、従来のCADでは作成が難しいような細かいラティスや、今回のようなトポロジー最適化を簡単に行うことができます。
詳しい製品概要は下記の商品ページよりご確認ください。
nTop紹介ページを見るまた弊社ではYouTubeにてトポロジー最適化について解説した動画も出していますので、こちらも参考にしてみてください。
弊社のYouTubeアカウント「テクノソリューションズの3Dデータ活用術」ではnTop関連動画を再生リストにまとめています。どうぞご覧ください。